DFS

DFS(Depth First Search) 

• 그래프 탐색 알고리즘으로, 그래프탐색이란 한 정점에서 시작하여 탐색 조건에 맞는 노드를 찾을때까지 모든 노드를 방문하는 방법입니다.
• 깊이 우선탐색으로 한 정점에서 탐색을 시작할때 하나의 Branch를 완전히 탐색 한 후 다음 Branch를 탐색하게 됩니다.
• 스택과 재귀로 구현이 가능합니다.

 

장점
단지 현 경로상의 노드들만을 기억하면 되므로 저장 공간의 수요가 비교적 적습니다.
목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있습니다.

단점
해가 없는 경로에 깊이 빠질 가능성이 있다. 따라서 실제로는 미리 지정한 임의 깊이까지만 탐색하고 목표 노드를 발견하지 못하면 다음 경로를 따라 탐색하는 방법이 유용할 수 있습니다.
얻어진 해가 최단 경로가 된다는 보장이 없다. 이는 목표에 이르는 경로가 다수인 문제에 대해 깊이우선탐색은 해에 다다르면 탐색을 끝내버리므로, 이때 얻어진 해는 최적이 아닐 수 있다는 의미입니다.

 

과정

※다음과 같은 그래프의 정점 1에서 모든 노드를 탐색 스택을 이용한 DFS를 하는 과정이고,

한번 방문한 노드는 방문처리가 되어 다시 방문 할 수 없다고 가정합니다.

오른쪽의 스택의 변화와 함께 보시면 이해가 편합니다.

 

 

 

 

 

1

스택

 

 

 

 

 

 

 

첫번째 노선인 1을 스택에 먼저 넣고 1과 근접하는 노드인 2를 찾아 스택에 넣습니다.

 

 

 

 

2

1

스택

 

 

 

 

 

 

스택의 가장 위에 있는 2에서 근접한 노드 3을 스택에 넣습니다.

 

 

3

2

1

스택

 

 

 

 

스택의 가장 위에 있는 3에서 근접한 노드 4를 스택에 넣습니다.

 

 

4

3

2

1

스택

 

 

 

 

여기서 스택의 가장 위에 있는 노드 4는 방문하지 않고 자신과 연결된 노드는 존재하지 않기 때문에 스택에서 삭제해줍니다. 그리고 3번노드 2번노드도 같은 상황이므로 스택은 다음과 같이 변화하게 됩니다.

	->		->
3
2		2
1		1		1

그리고 다시 노드 1로 돌아가서 1과 연결된 노드 5를 스택에 넣습니다.

 

 

5

1

스택

 

 

 

 

 

 

 

 

스택의 가장 위에 있는 5에서 근접한 노드 6를 스택에 넣습니다.

 

 

6

5

1

스택

 

 

 

 

 

스택의 가장 위에 있는 6은 방문하지 않은 인접 노드를 가지지 않기 때문에 스택에서 삭제되고,

5번에서 다시 방문하지 않은 근접노드를 찾아서 7번을 스택에 넣습니다.

 

 

 

 

7

5

1

스택

 

 

 

 

스택의 가장 위에 있는 7에서 근접한 노드 8를 스택에 넣습니다.

 

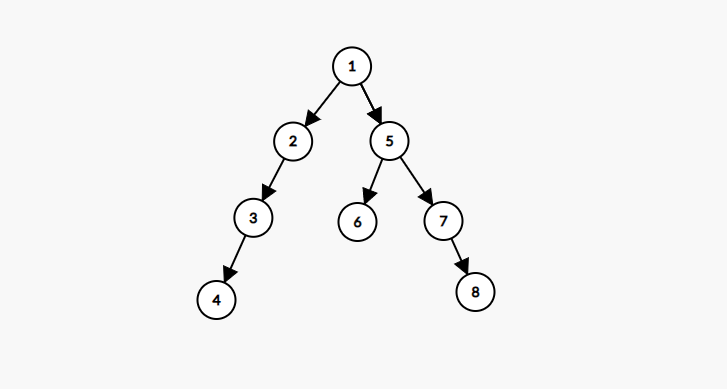
8

7

5

1

스택

 

 

 

 

이제 모든 노드를 방문했기 때문에 자연스럽게 스택의 가장 윗부분 부터 차례대로 비워지게 됩니다.

 

코드

위의 과정을 코드로 구현한 것입니다.

#include <iostream>
#include <vector>
#include <stack>
using namespace std;


bool visited[8];
vector<int> graph[8];
stack<int> stk;

// 스택으로 구현
void dfs(int num)
{
	stk.push(num);
	int current;
	while (!stk.empty())
	{
		current = stk.top();
        stk.pop();
		cout << current;
		visited[current] = true;
		for (int i = 0; i < graph[current].size(); i++){  //연결된 노드가 있을때
			int next = graph[current][i];
			if (!visited[next]) // 방문하지 않았을때
            	stk.push(current);
				stk.push(next);	//스택에 추가
		}
	}
}

/*  재귀로 구현    
void dfs(int current)
{
	visited[current] = true;
	cout << current << " ";
	for (int i = 0; i < graph[current].size(); i++){	// 연결된 노드가 있을때
		int next = graph[current][i];
		if (!visited[next]) // 방문하지 않았을때
			dfs(next);		// 재귀 호출
	}
}
*/

int main(void)
{
	//그래프 정의
	graph[1].push_back(2);
	graph[1].push_back(5);

	graph[2].push_back(3);

	graph[3].push_back(4);

	graph[4].push_back(5);

	graph[5].push_back(6);
	graph[5].push_back(7);
		
	graph[7].push_back(8);

	dfs(1);
}

재귀함수로 구현시 스택오버플로우를 주의해야합니다.

DFS는 백트래킹기법과 함께 사용하여 각각의 Branch의 탐색 속도를 높일 수 있으며, DFS를 이용해 위상탐색을 구현할 수 있으니 공부해보시는 것도 괜찮을 것 같습니다.

 

DFS 관련 문제를 풀 수 있는 곳입니다.

https://www.acmicpc.net/problemset?sort=ac_desc&algo=127

문제 - 1 페이지

 

참고

https://namu.wiki/w/%EA%B9%8A%EC%9D%B4%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89?from=DFS